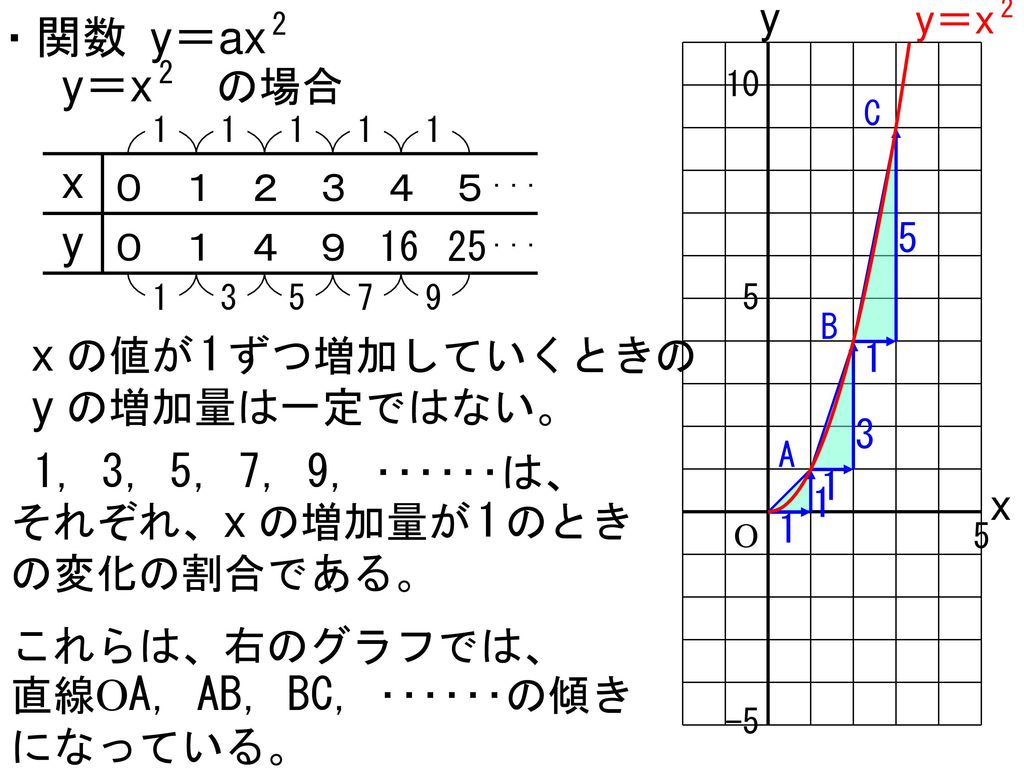
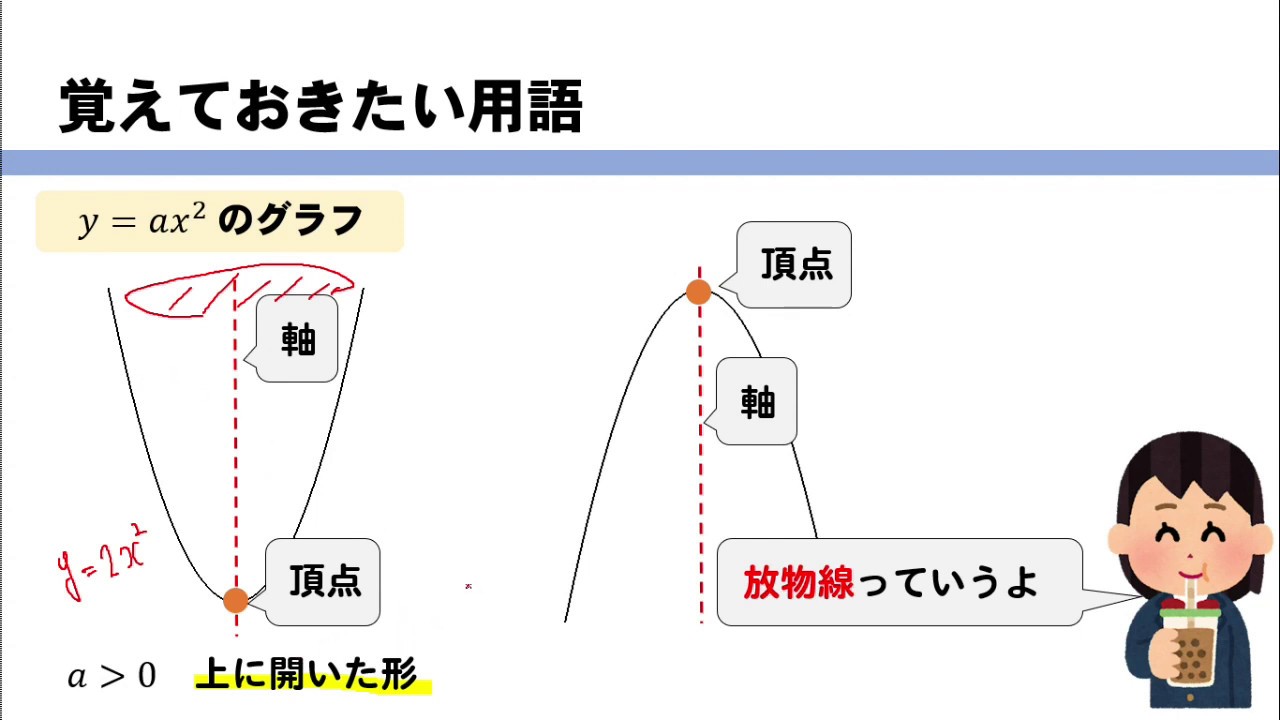
コレクション y=ax二乗 グラフ 680799-Y=ax二乗 グラフ
2次関数の基本
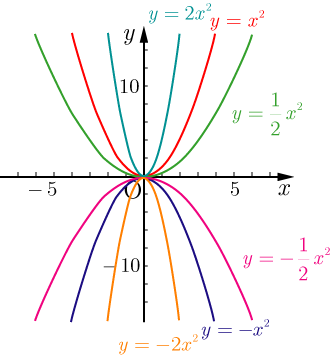
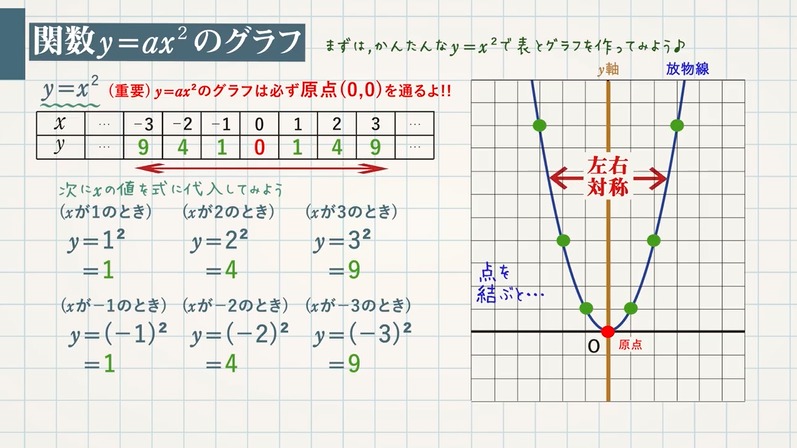
Josspixskqr 最新 y=ax二乗 グラフ 5436Y=ax二乗 グラフ y=ax 2 のグラフとy=ax 2 のグラフはx 軸について対象である。 練習問題をダウンロード *問題は追加します。しばらくお待ち下さい。 2乗に比例する関数のグラフの特徴 *18/8/29 1のプリントの問題、解答の文字が見づらくなっていましたので修正しました。 Facebook;
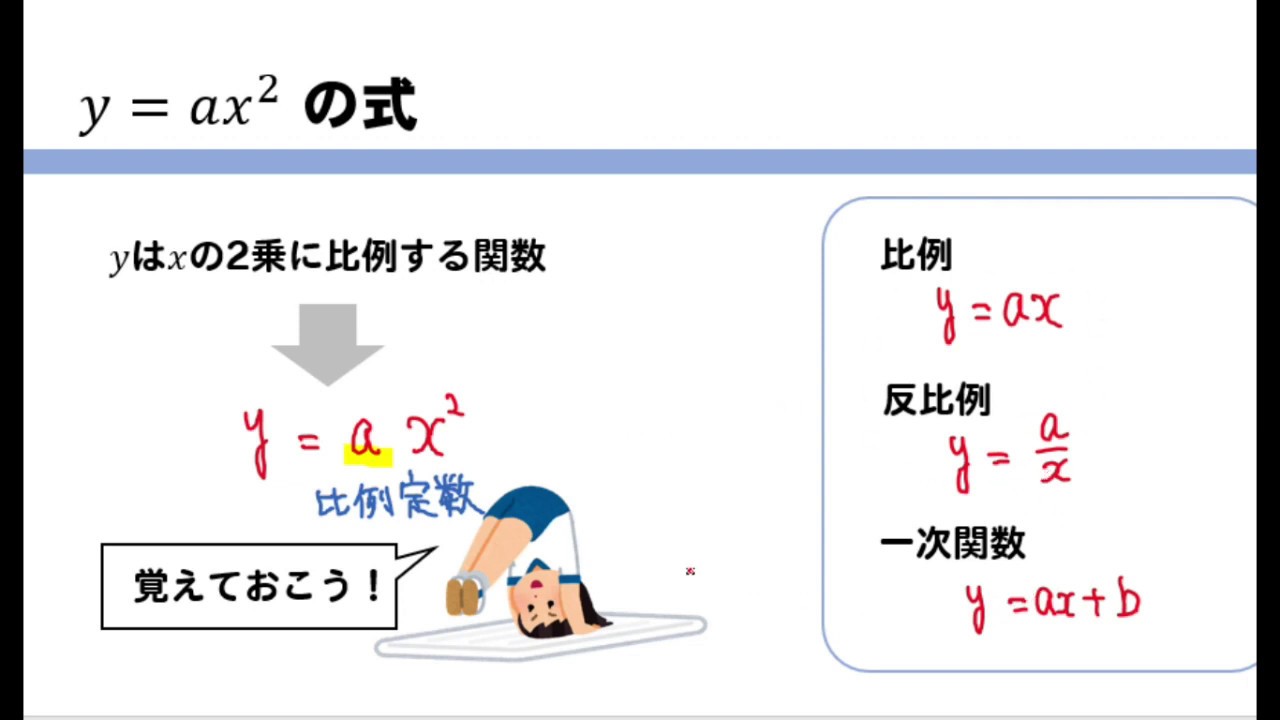
Y=ax二乗 グラフ
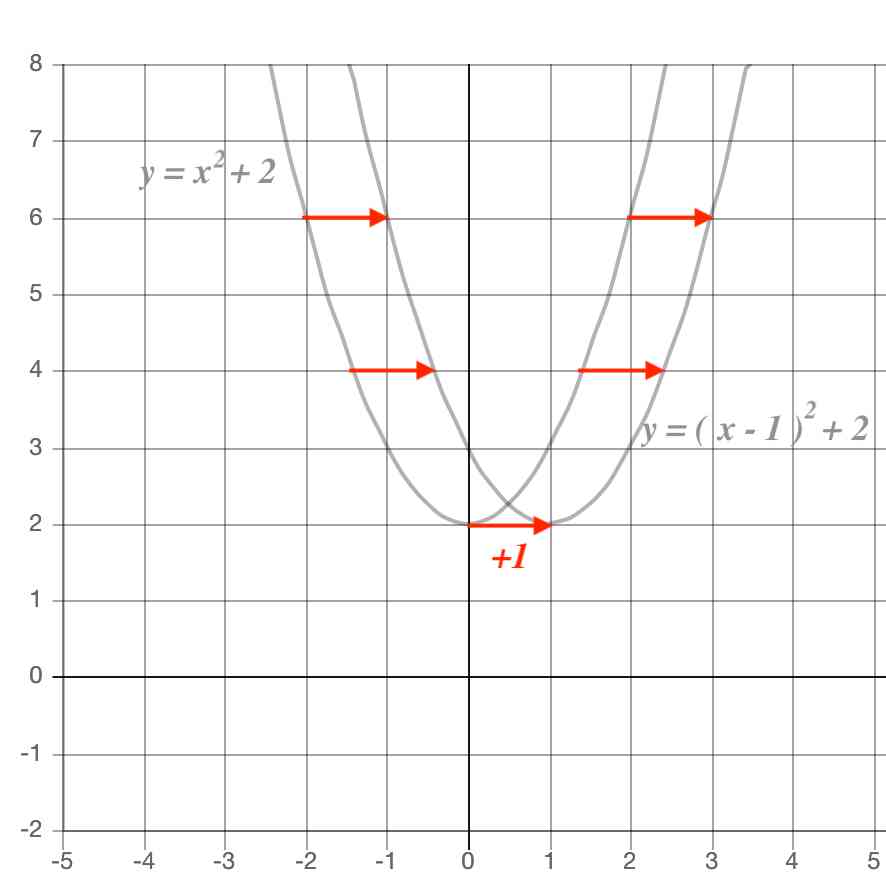
Y=ax二乗 グラフ- 最終的には、二次関数 y = ax2 bx c y = a x 2 b x c のグラフを考えるのですが、いきなり考えるのは難しいです。 しかし、簡単なケース y = ax2 y = a x 2 から出発して(参考: 基本二次関数 y=ax^2 のグラフ )、このグラフを平行移動する、という順番で考えると、一般的なケースでも対応できるようになります。 グラフの平行移動を考えていく前に、まずは、点の移動に関数 関数y =ax2のグラフ(4) 1 関数y =ax2のグラフが次の点を通るとき,この関数の式を求めなさい。 (1)点(2,16) (2)点(3,−18) (3)点(−2,12) (4)点(−3,−9) 2 関数y =ax2のグラフが点(2,−4)を通る。このグラフが点(−3, m,)を通るとき, mの値を求めなさい。 3 関数y =ax2のグラフが3点(2,−8),(3,b),(c,−2)を通る

関数y Ax2乗 変域の求め方 変域から式を求める問題を解説 Youtube
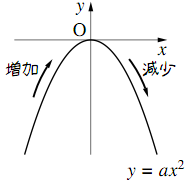
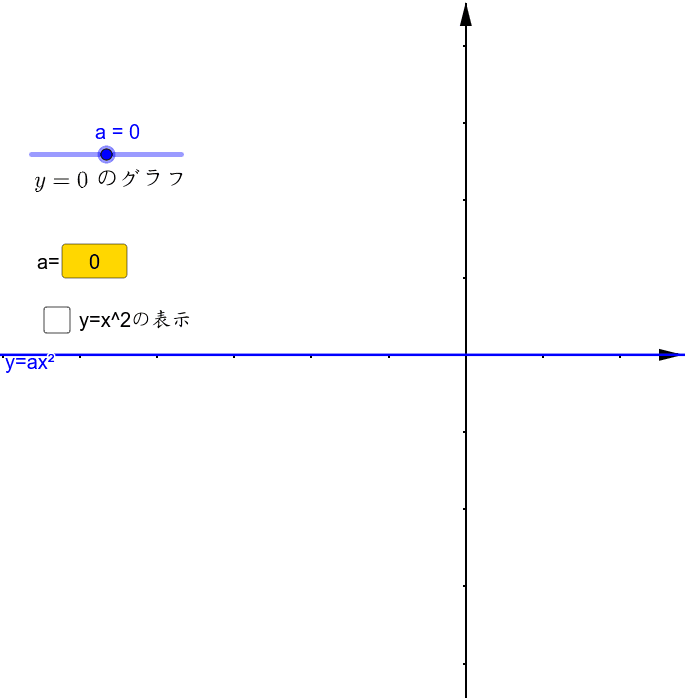
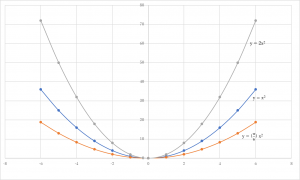
y=ax^2のグラフ 比例反比例や一次関数に続き、再びグラフが出てくる。 しかも直線ではなく、放物線である。 放物線とは、まぁボールを斜めに放り投げた時の軌道だと思えばいい。 我々ジャグラーにはなじみ深いものである。 以前も習ったことだが、再(問)y=x(2)axa8のグラフが次のようになる定数aの値を求めなさい。 質問<3374>3の男「2次関数」 xの2次関数f(x)=x^22ax2a^24があり、y=f(x)のグラフはx軸と異なる2点で交わる。 ただし、aは定数である。 (1)y=f(x)のグラフの頂点の座標を求めよ。また、aの値の範囲を求めよ。 質問<3259>おばさま問題一括 (6,604Kb) 解答一括 (7,191Kb) 関数 y=ax 2 (2) 関数 y=ax 2 のグラフ (1) 関数 y=ax 2 のグラフ (2) 関数 y=ax 2 のグラフ (3) 関数 y=ax 2 のグラフ (4)
グラフの読み取り \(2\) 乗に比例(\(2\) 次関数)のグラフを読みとることも、非常に重要です。 例題1 下の図の放物線の式を求めなさい。 解答 原点を通る放物線なので、 放物線の式は \(y=ax^2\) となりY=ax二乗 Y=ax二乗 グラフ 最小二乗法 擬似逆行列 下のサイトの説明を読んで最小二乗法の勉強をしています。 未知パラメータxが1個(N=1)、出力yが10個(M=10)のとき、 擬似逆行列を求めようとすると、(A#A)^1 が1×1行列になってしまいます。練習の解説授業 「y=ax 2 +bx+c」 のグラフをかく問題だね。 手順は以下の通りだよ。 POINT 平方完成して頂点を求めよう! 平方完成のポイントは、 「最初にくくる」 こと、そして、 「xの係数を半分にして2乗」 だよ。 よって、 y=-x 2 +2x+4 =-(x 2 -2 x)+4 =-(x -1 ) 2 +1 +4 =(x-1) 2 +5 よって、頂点は (1,5) だね。 放物線の向きを確かめよう! y= -x 2 +2x+4
Y=ax二乗 グラフのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 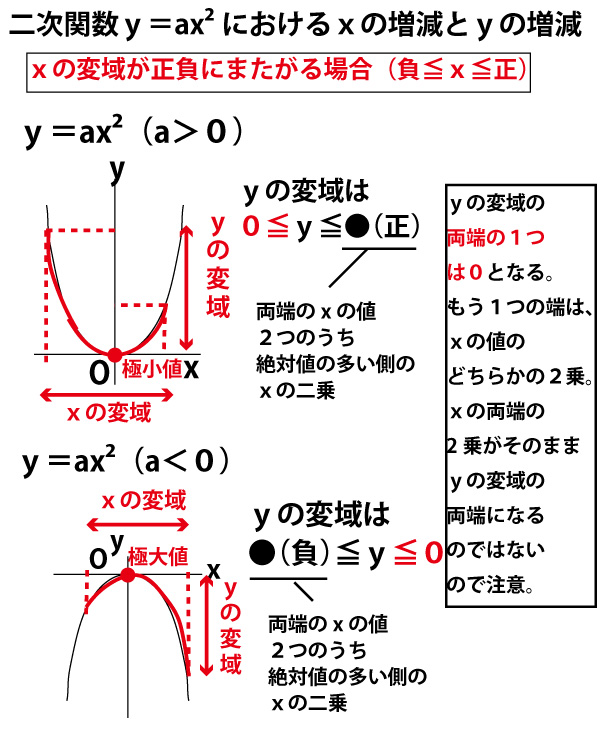 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 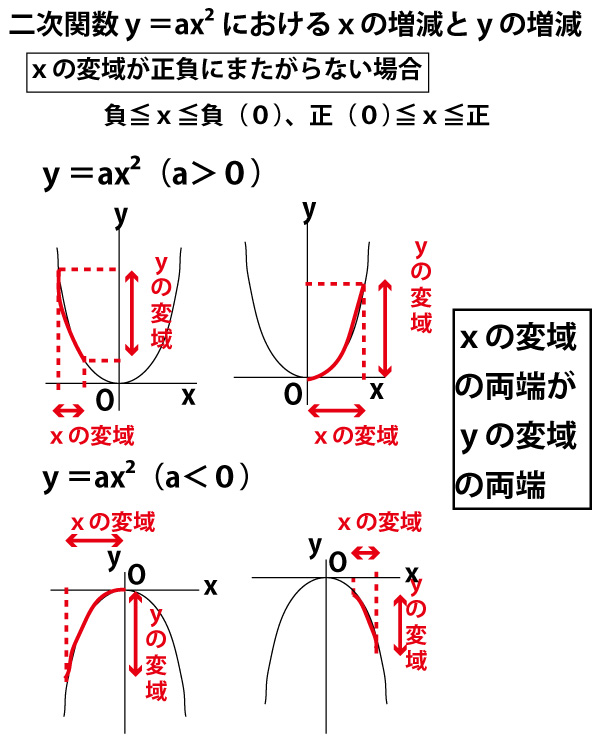 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 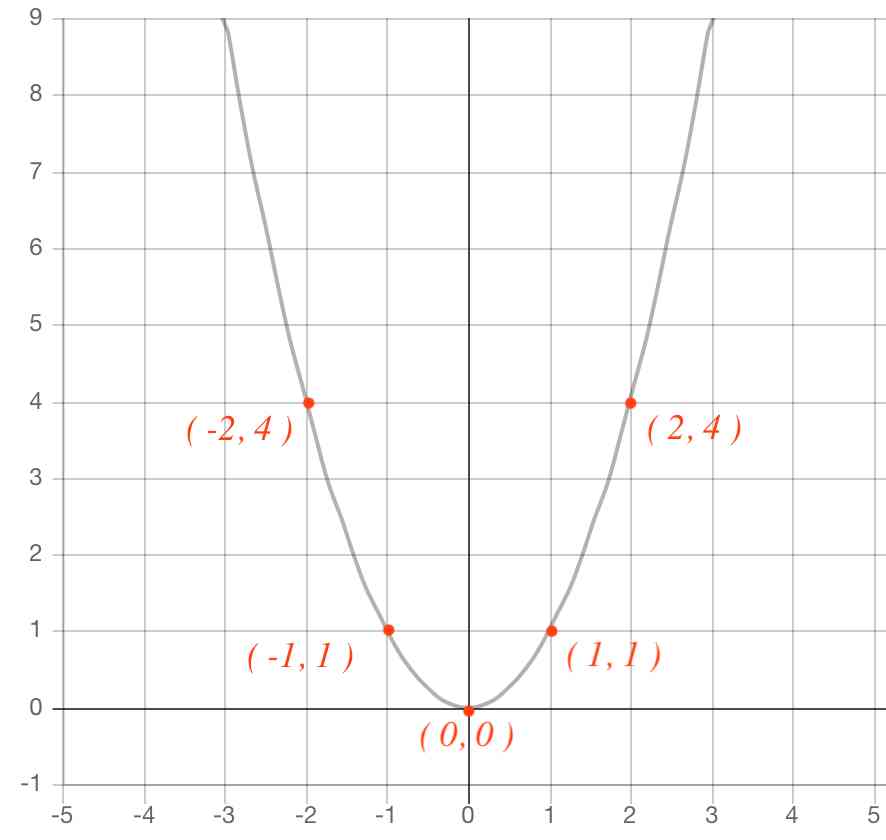 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 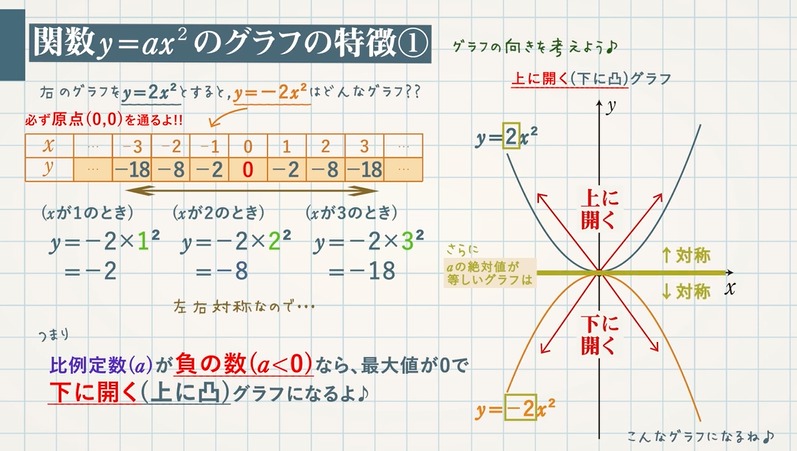 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 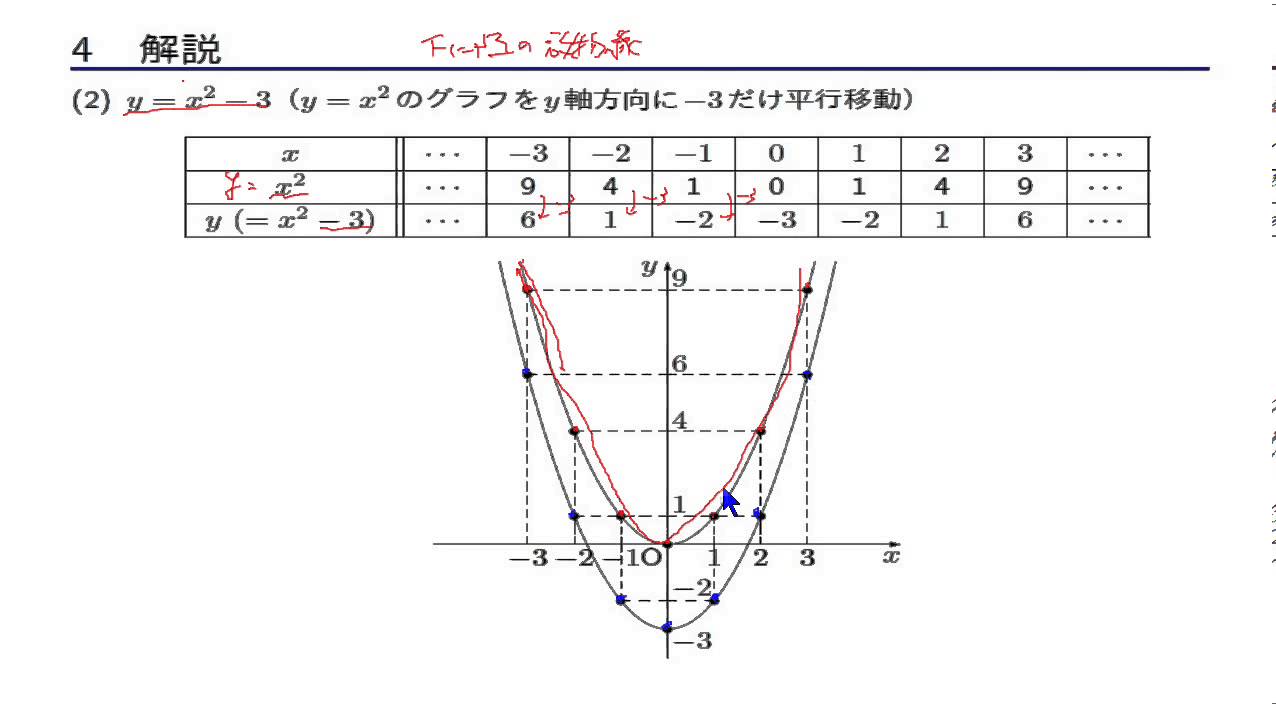 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 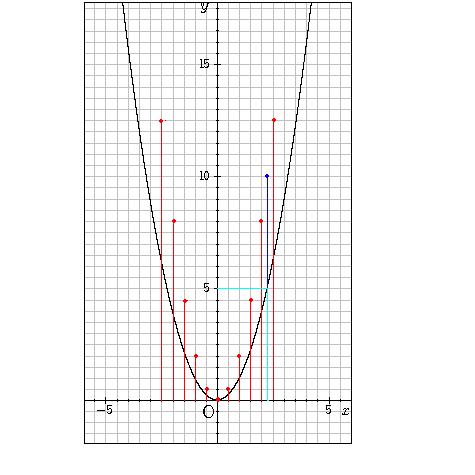 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 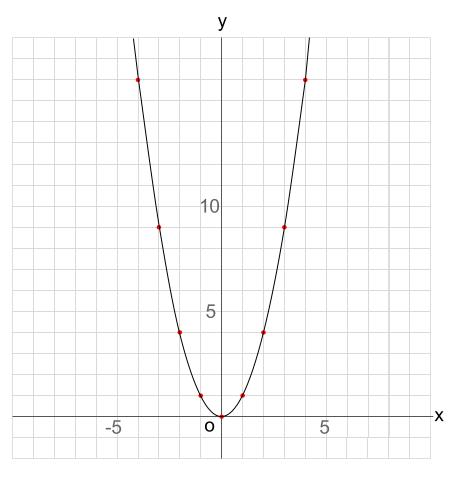 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
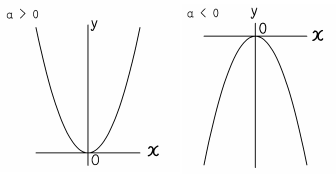 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 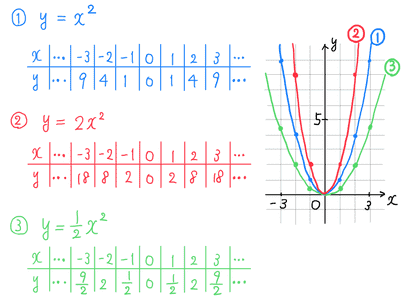 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 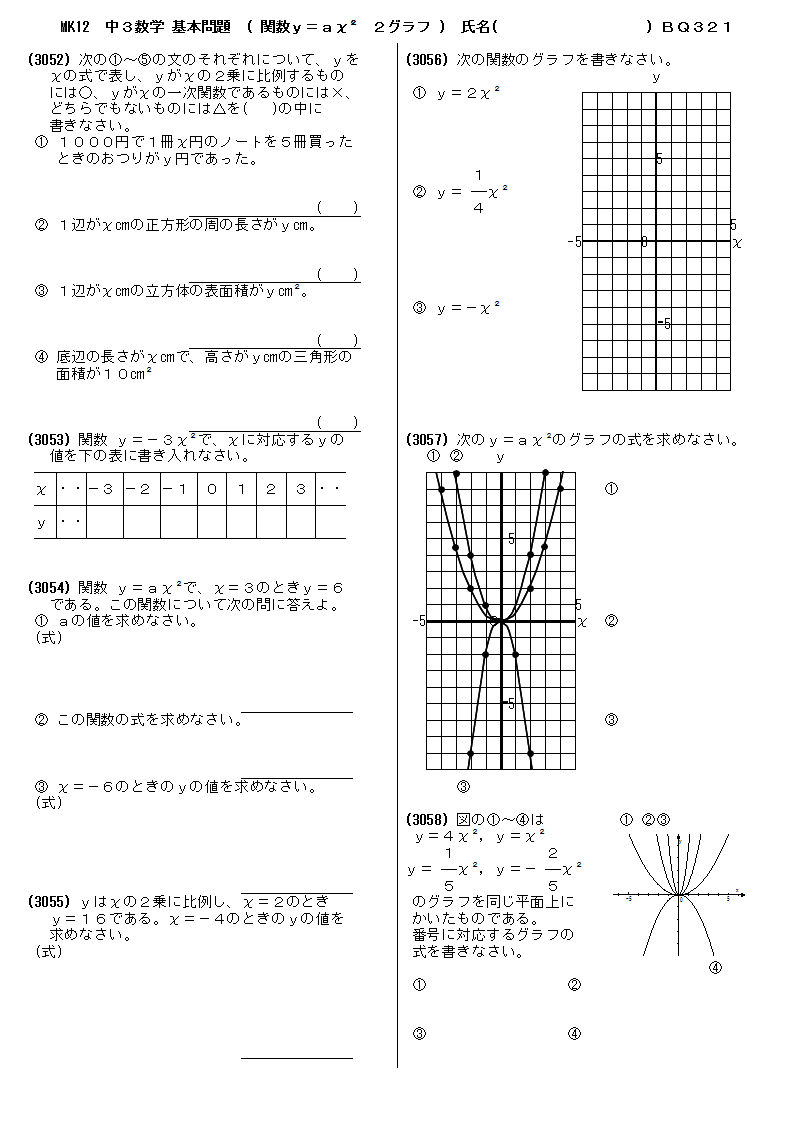 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 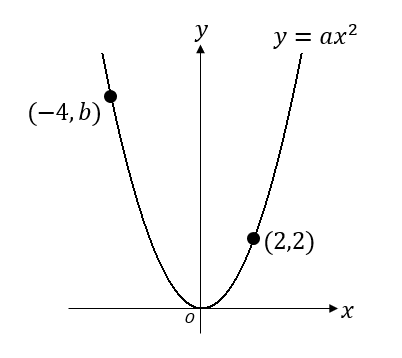 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 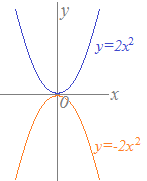 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 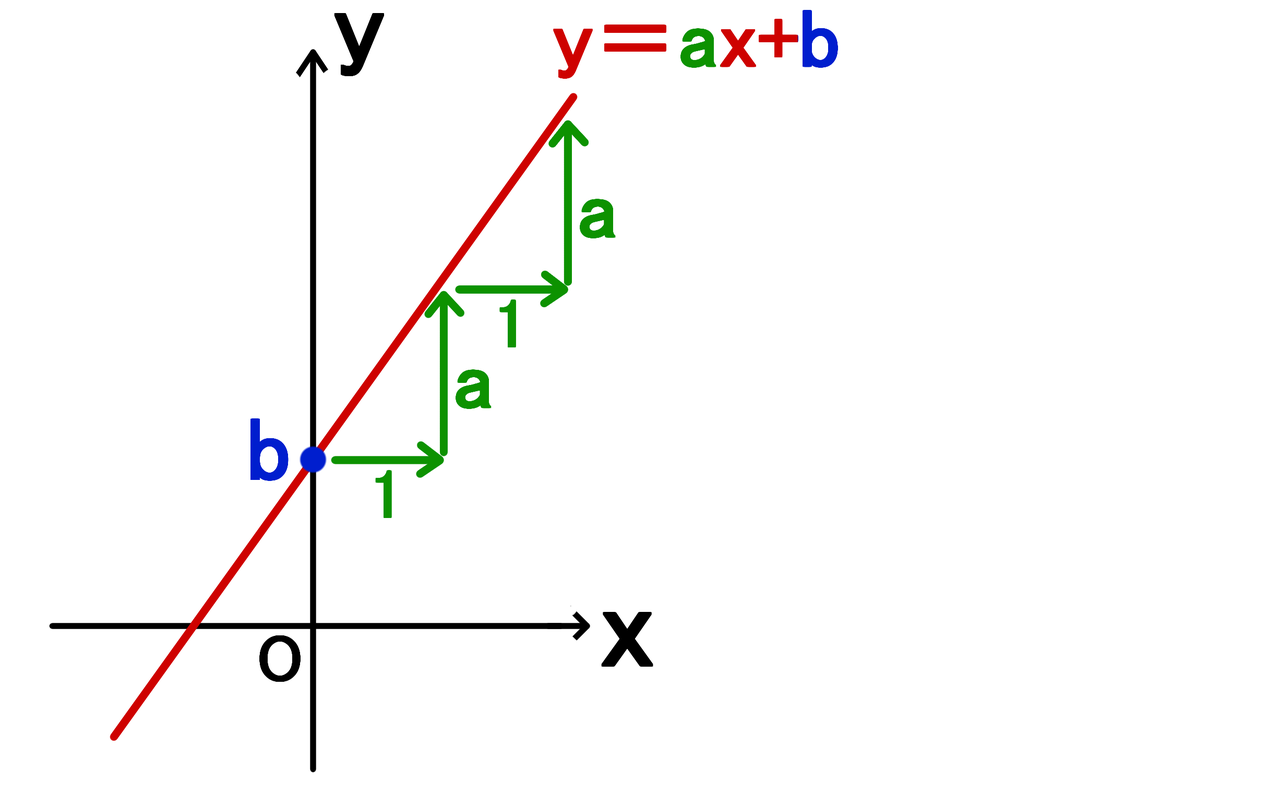 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 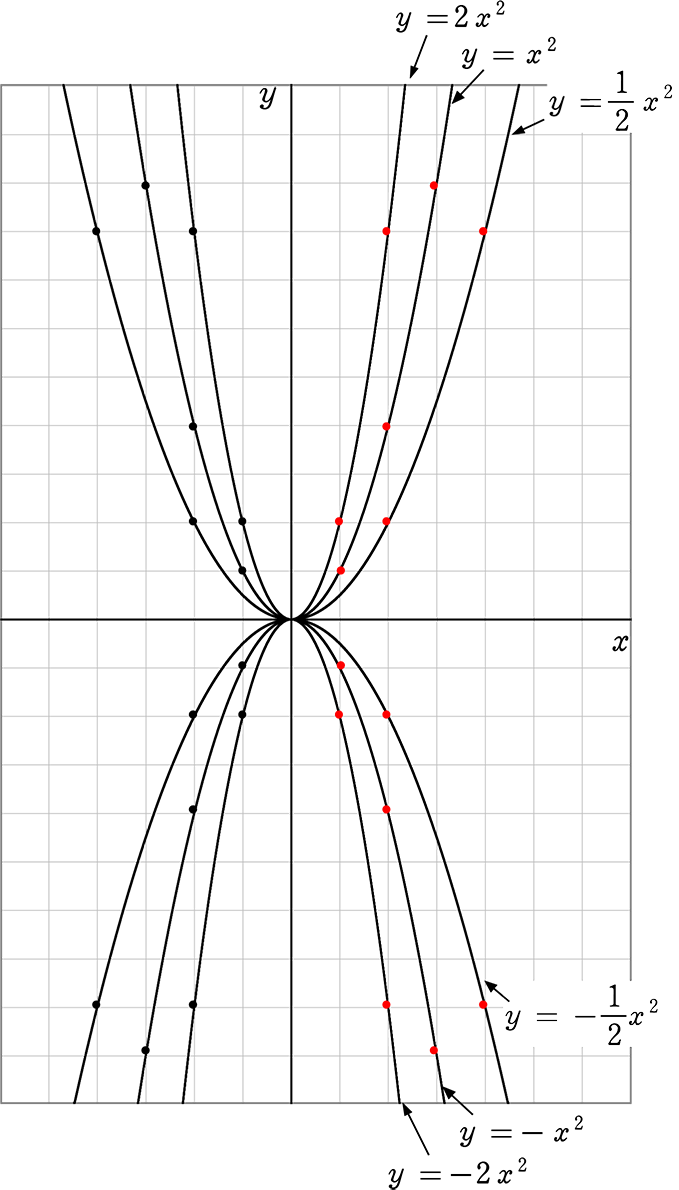 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 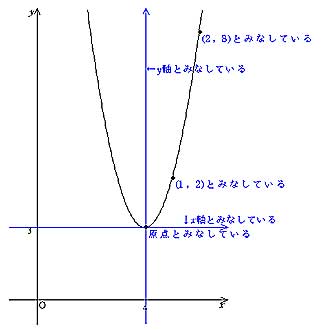 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 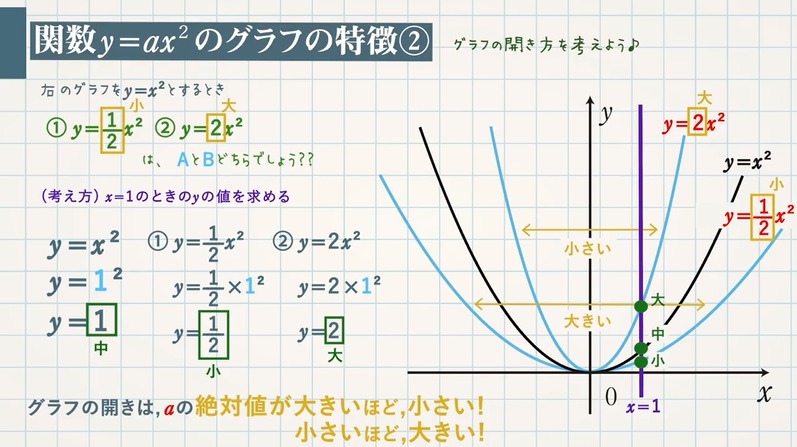 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 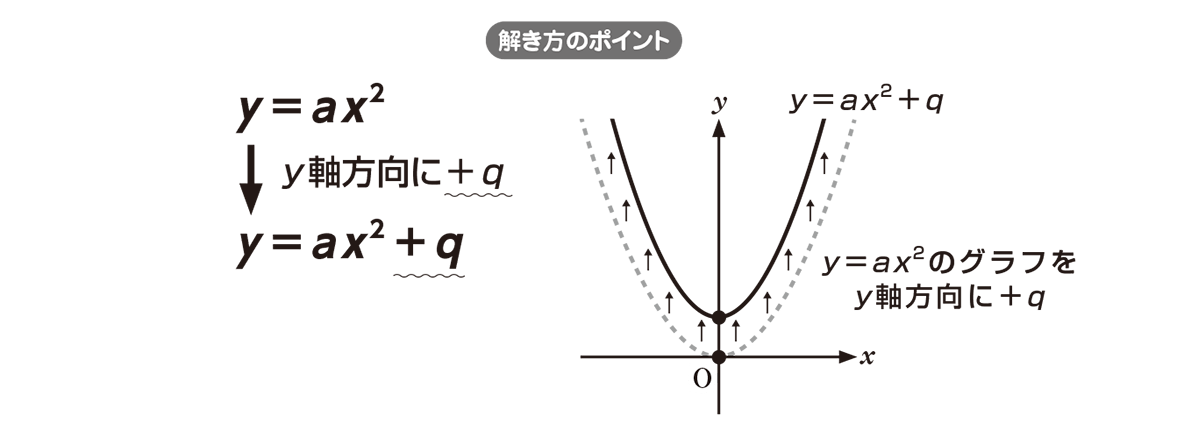 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 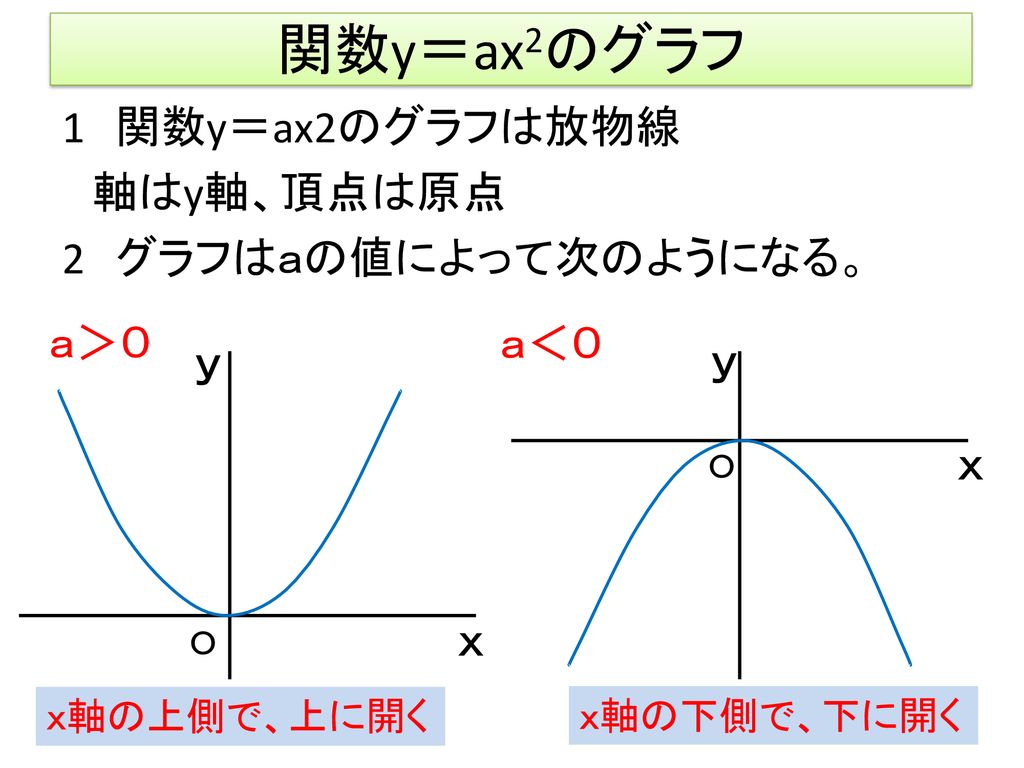 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 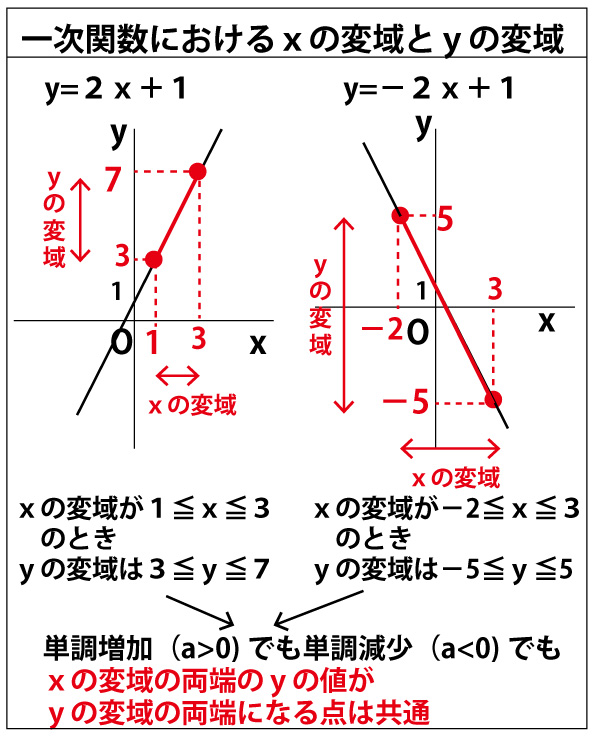 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 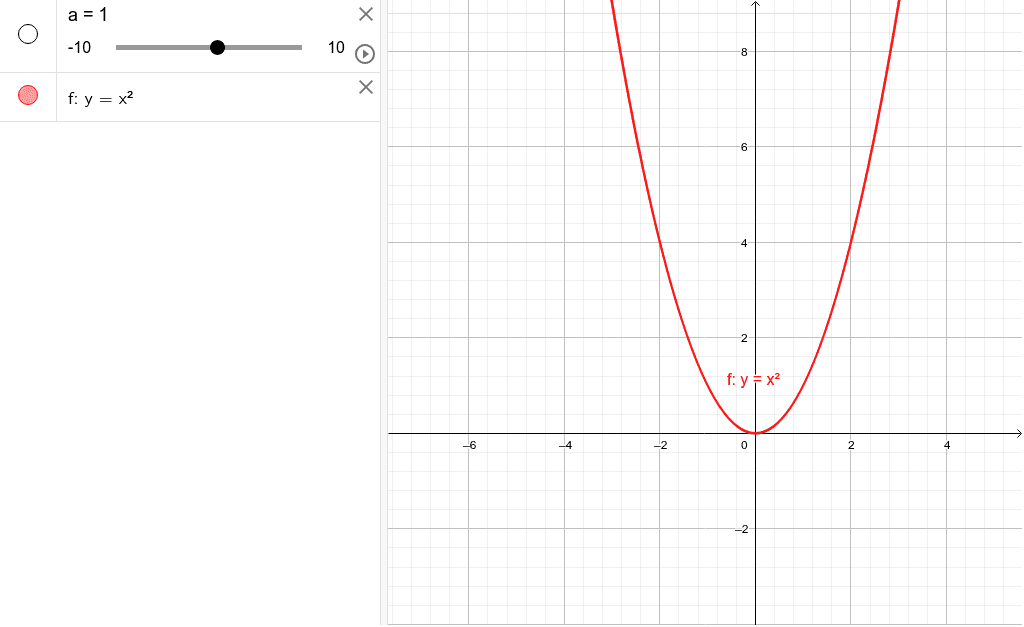 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
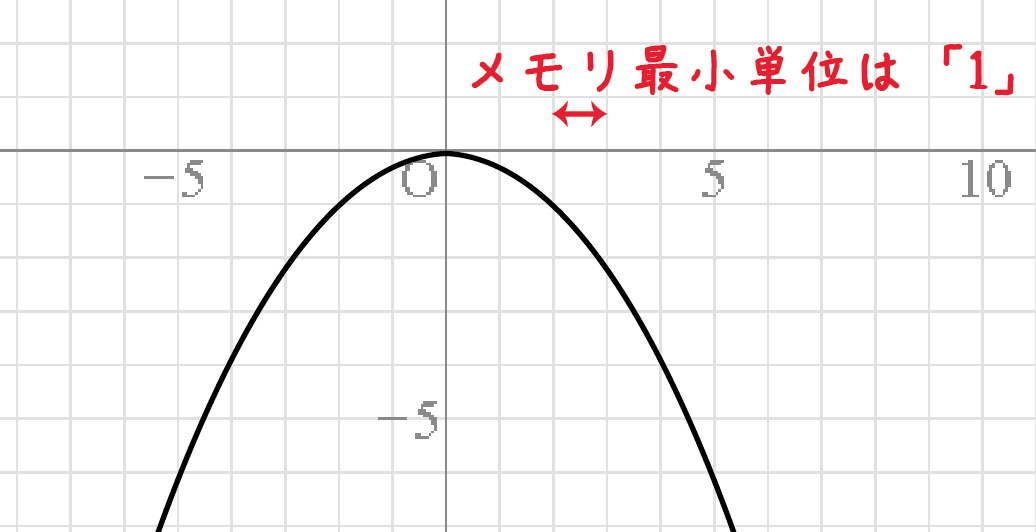 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 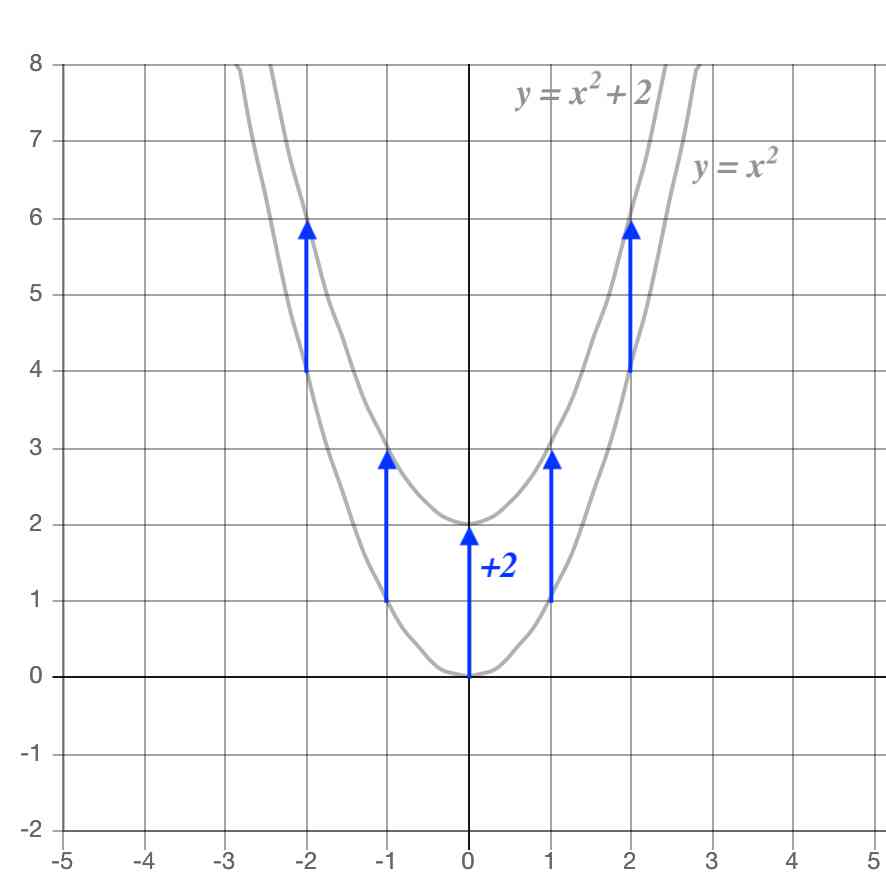 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 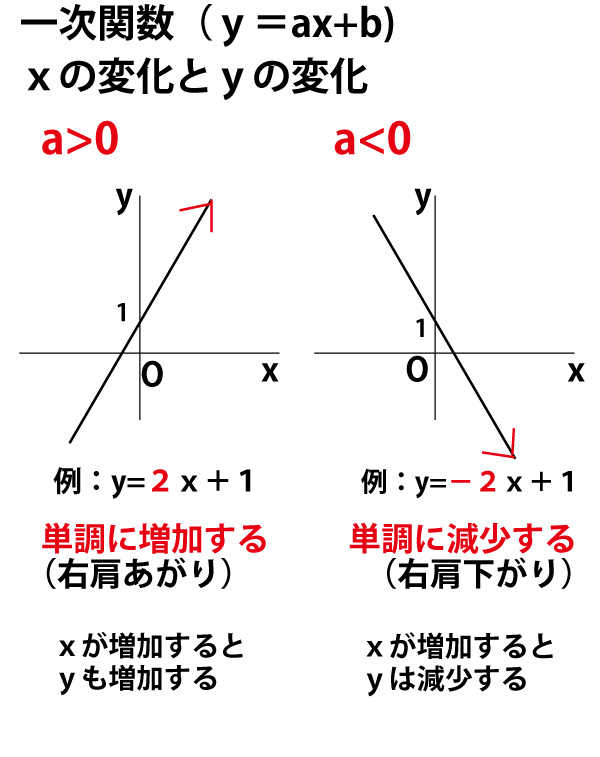 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 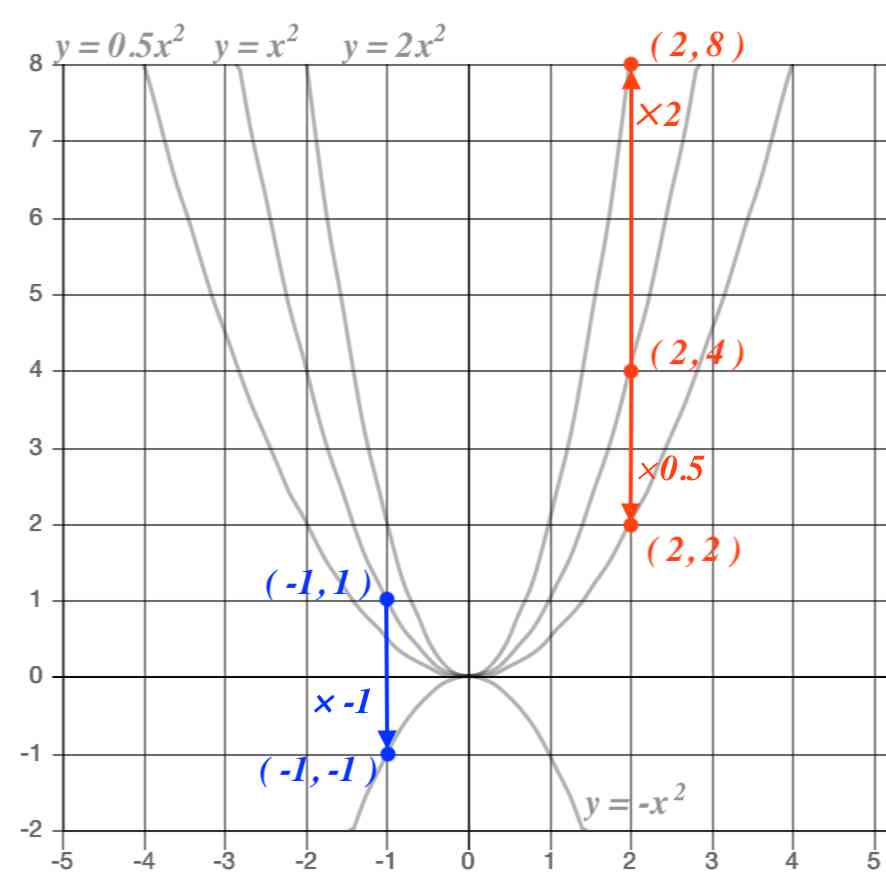 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 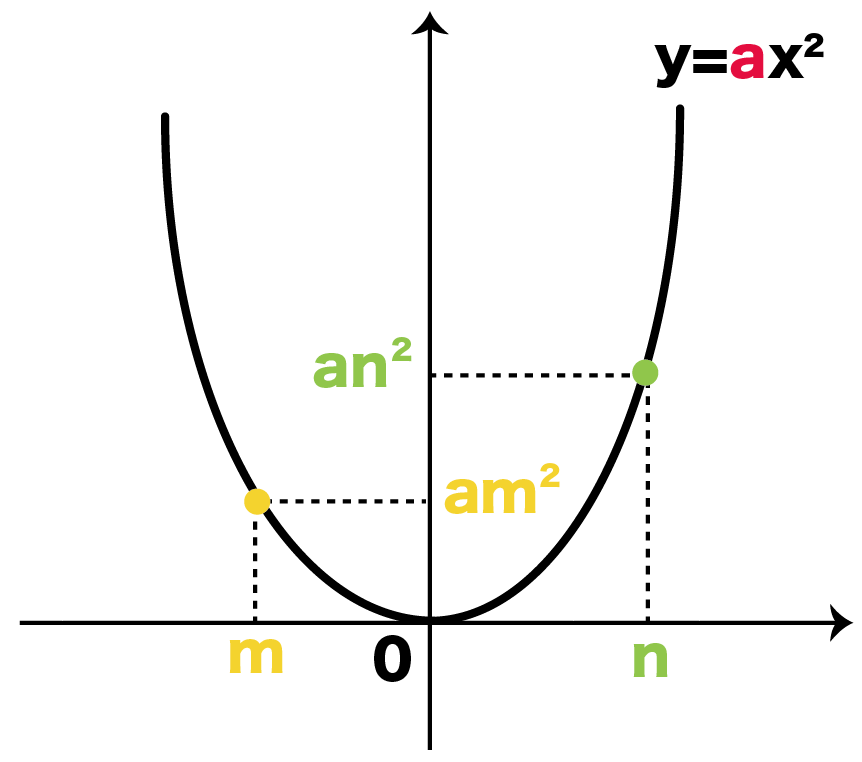 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 | 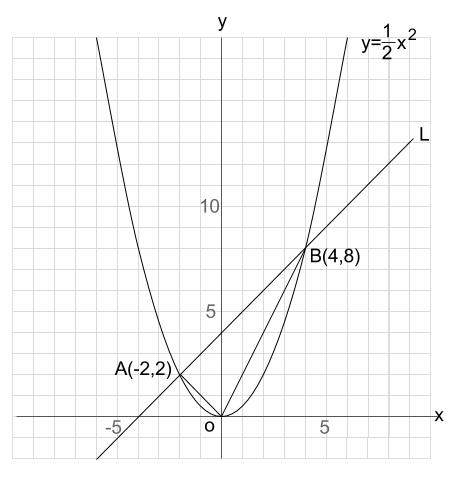 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |  2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 |
一次関数の式「y = ax b」に切片と座標を代入してやればいいんだ。 そんで、できた方程式を解いてやれば直線の式が求められるね。 例題では、 切片:3 座標(2, 11) だったね? 切片の「3」をy = axbに代入してみると、 y = ax 3 になるね。問1 y=2x 2 のグラフ上に2点A,Bがあります.A,Bの x 座標がそれぞれ −1, 2 であるとき,次の問いに答えなさい. (1) 2点A,Bの座標を求めなさい. (2) 2点A,Bを通る直線の方程式を求めなさい. (3) 2点A,Bを通る直線が y 軸と交わる点Pの座標を求めなさい.
Incoming Term: y=ax二乗 グラフ, y=ax二乗 グラフ特徴, y=ax二乗 グラフ 書き方, y=ax二乗+bx+c グラフ, y=ax二乗+b グラフ,
コメント
コメントを投稿